Strike Selection Criteria

USING OPTION SPREADS FOR STRIKE SELECTION

Last Updated

March 24, 2023

By Andres Talero

Overview

This article outlines two methods for identifying optimal option strikes. Both methods are based on vertical option spreads pricing relationships. Option spreads are presented as marginal measures of risk. Two different criteria to select option strikes are outlined. The first method is based on arbitrary utility preferences, while the second one uses the change in slope of the options price curve.

Relevance of Strike Selection

Strike selection is an important step when constructing or rebalancing options strategies. The potential choice of strikes is a large set even within a single chain of listed options (all same underlying puts and calls available for a single expiration).

Developing consistent rules across a set of option strategies facilitates portfolio construction, rebalancing, and automation. It also simplifies modeling and decision processes.

Using the marginal cost of options is particularly relevant when analyzing spreads and other option strategies using two or more options – where the relative value of the options in a strategy is key. Other simple approaches to strike selection – not discussed in this article - include absolute premium levels, the distance between market price and strike, and using at the money premiums as yardsticks.

Vertical Option Spreads

Pairs of same expiration options such as put spreads and call spreads are popular option strategies when taking directional views. The strategies considered in this article involve the simultaneous purchase and sale in a 1 to 1 ratio of same expiration date options with different strikes – in particular bull call spreads (the simultaneous purchase of a lower strike call and sale of a higher strike call, both with the same expiration); and bear put spreads (the purchase of a higher strike put, and sale of a lower strike put).

Option Spread Payouts

The maximum payout of directional option spreads is equal to the difference between the strikes of the two options used to construct the spread. Both a 100 to 110 call spread or put spread will have a maximum payout at expiration of 10, determined by the difference between the strikes. Spread payouts exhibit symmetry. For a given pair of vertical spreads with the same high and low strikes, the sum of payouts of a bull call spread and a bear put spread is equal to the value of the range.

Example of Option Spreads and their payouts

It is useful to think about the net premium of a vertical spread as the percentage cost of a contingent payout - the totality of the option spread - occurring when the two options expire in the money. In addition, converting net premiums into percentage costs facilitates comparisons within individual option chains, across option chains and for different underlying assets.

For example, if a 100 strike call costs $12; and the same expiration 110 strike call costs $8, the net premium of a bull call spread using the two options is $4, with a maximum payout of $10. Dividing the net premium ($4) by the difference between the two strikes ($10) yields a percentage measure of the cost of the strategy (40%), assuming the maximum payout is realized. The 100 to 110 bull call spread, with a cost of $4, can also be thought to cost 40% of the range (=$4/10).

Percentage costs can be calculated in similar fashion for put spreads. The combination of a 110 strike put with a $18 premium, and a 100 strike put with a $12 premium results in a net premium of $6 for the 110 to 100 put spread, or 60% of the spread ($6/10).

Option Chain example

Option chain premiums for listed strikes are available from exchanges, broker dealers, and financial websites such as yahoo finance and marketwatch. Prices in an option chain comprise all same underlying puts and calls available for a single expiration. Chain strikes are discrete, as for each expiration date there is a limited set of options in any chain offered by an exchange.

Simplified Example Option Chain Table. Hypothetical Stock trading at a 100 price, interest rates of zero; no dividends.

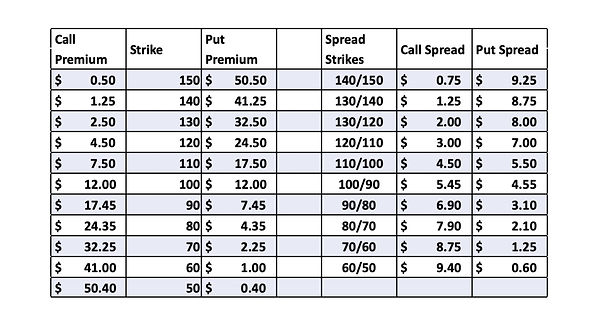
The spread columns - right-side in the option chain example - are calculated by taking the difference between the premiums from premium columns to the left of the table.

Vertical spreads as measures of marginal cost and return

Vertical option spreads capture the difference between option premiums when comparing two option strikes for pairs of calls or puts with the same expiration. The percentage cost of any spread (two puts or two calls) can also be calculated dividing the net premium by the difference between the strikes. It reflects the increased percentage cost (additional premium) for having a potential higher payout equal to the difference between the strikes.

Option spreads can be thought of as a measure of the directional marginal cost between two strikes.

When comparing two calls with the same expiration, purchasing a lower strike call increases the potential payout by the difference between the higher and lower strike being considered. The premium difference (increase in premium for a lower strike call) is a measure of the marginal cost of choosing between the two strikes.

By the same token, when comparing two puts with the same expiration, purchasing a higher strike put increases the potential payout by the difference between the higher and the lower strike being considered. The premium difference (increase for a higher strike put) is a measure of the marginal cost of choosing between the two strikes.

Option spreads of the same magnitude (difference between strikes) have lower net premiums as the observed strikes move away from the at the money price. Spreads (bear) between lower strike puts command lower net premiums compared to put spread premiums for higher strikes. By the same token, higher strike call spreads (bull) command lower net premiums than lower strike call spreads.

Utility approach to strike selection

The utility approach sets an arbitrary maximum price to be paid for unit of marginal risk or of potential return. The choice of level is explicitly arbitrary and based on investor preferences. Once a marginal level has been set, it is straightforward to find the option spread that most closely meets the criteria. Each spread cost is determined by the relative value of options in the chain. The spread meeting the criteria and with strikes closest to at the money (where puts and calls premiums are the same) is chosen.

At a portfolio level, and across time, the general concept is to set a level and apply it consistently - when entering new positions or rebalancing existing ones.

Put strike selection example.

Consider an investor long a stock and choosing the strike for a put to hedge the position (a protective put strategy). To choose the strike of the put to purchase, the investor may elect to use a set percentage cost for the marginal unit of risk being reduced, as observed from the cost of put spreads in the option chain. In this case, when comparing to same expiration put strikes, the marginal risk being reduced is the premium difference between the higher and the lower strike.

Assume the investor sets the criteria for selecting a put strike at a 10% marginal cost. The highest strike put that has an absolute cost of less than 10% of its strike is a 90 Strike put, with a $7.45 premium (approximately 8.3% of the strike). But using an absolute premium level only looks at a single strike. Notice that the bear put spread between the 90 strike and the next lower strike in the chain (80) costs 3.10 (or 31% of the spread between the 90 and 80 strikes, so the marginal cost of hedging between the 90 and 80 strikes is 31%, well above the 10% marginal cost criteria.

In the example table the highest strike put meeting the 10% marginal cost criteria corresponds to a put with a strike of $60, with a $1 premium. The marginal cost - the option spread - to the next lower put (the 50 strike) is $0.6, or 6% of the 60/50 put spread in the table.

Since the marginal cost choice is arbitrary, a different investor may choose a 25% marginal cost as criteria, resulting on a higher put strike for the same example table; a strike of 80 - at which the bear put spread to the next lower strike falls below 2.5 for a 10 spread between the strikes. The investor using the 25% criteria would purchase the 80 put paying a premium of $4.35, with a 21% marginal cost, as observed from the 80 to 70 put spread, which costs $2.1

Call strike selection example.

The marginal cost criteria set in the above example can be restated for an investor purchasing a call. The investor may set a minimum marginal potential return when selecting the strike of the call being purchased - a set percentage cost for the marginal unit of potential payout, as observed from the net premium of call spreads in the option chain.

Assume the investor sets a 10% minimum marginal return criteria.

In the example table the lowest strike call meeting the marginal return criteria corresponds to a call with a strike of $60, with a $41 premium. The marginal return of the option spread to the next higher call (the 70 strike) is $8.75, or 88% of the 60/70 call spread in the table.

An investor choosing a minimum 25% marginal return level as criteria for choosing a call from the same example table, will choose the call with a strike of 80 - at which the net premium for the bull call spread to the next higher strike falls below 75%. The call has a premium of $24.35, with a 31% marginal potential return, as observed from the 80 to 90 call spread, which costs a net premium of $6.9, or 69%.

Because of payout symmetry of call spreads and put spreads for a given expiration, choosing a maximum marginal cost for puts and a minimum marginal return for calls, results in the same strike selection for puts and calls, after adjusting the premiums to future value.

The utility approach is usually very simple to implement once a criteria level is chosen, and can be easily standardized at a portfolio level. It can also be directly connected to minimum return and cost of capital concepts. Using the criteria requires little information to keep track of. Its main drawback is its arbitrary nature.

Premium price function inflection point approach.

A second method for identifying optimal strikes is to look at the change in net premiums of option spreads. Conceptually the idea is to identify out of the money strikes around which option spreads net premiums stop dropping.

Option pricing is usually performed using a mathematical function, which incorporates market information as an input and produces as an output option premiums for a given expiration. For listed options trading in the public market, the output of the option price function can be observed directly – it is the premiums of puts and calls for each strike in any given option chain. Observing changes across an option price function involves calculating the difference in option premiums across strikes – in the same manner as performed in the table example of this article.

Compared to the utility approach, the inflection point approach selects strikes based on the shape of option price curve, and not individual preferences. Both approaches are similar in that they use a marginal cost/return criteria to arrive at strike selection.

The inflection point approach has an important advantage. Around inflection points in the price curve the price function is expected to behave differently depending on the direction in which the underlying moves.

To illustrate this point, consider an investor purchasing a call option with a strike around the inflexion point. If the underlying moves up, the call option is expected to quickly appreciate; but if the underlying falls, the call is expected to fall in price at a lower speed. Depending on the context, this effect may be referred to as “convexity” or as “gamma”. All options have a degree of gamma – but the effect is highest around inflection points.

An inflection point criteria makes intuitive sense in a trading optimization context, but can be difficult to tract and implement consistently at a portfolio level. The marginal cost of options at an inflection point is sensitive to volatility, time to expiration and skews, making it difficult to consistently link inflection points to measures of cost and return of capital. Finding inflection points in a discrete option chain requires comparing different option spreads. It can be tricky for low strikes of a volatile underlying, or if the chain has few strikes. For over the counter options, determining inflection points requires the correct formulation of a premium function for all the relevant strikes.

Inflection points frequently fall somewhere around 2 and 3 at the money premiums from the at the money strike and at marginal premium costs ranging from 10% to 30% of the strike difference. Volatile underlying long term options can exhibit high at the money premiums as a percentage of the underlying's market value - which can distort low strike options and make inflection points difficult to observe because of the limited number of discrete strikes.

Using the two criteria in conjunction

Context, experience, risk preferences and investment style can guide the selection of specific strikes. The two methods outlined do not propose any break in arbitrage relationships or miss pricing of options - and a better understood as basic tools for strike selection. They are least useful in the context of short term directional views, where the at the money strike might in many cases be the obvious choice of strike, and an option spread might not be the desired strategy. They are most useful in a context of consistent portfolio risk optimization, where a single criteria across different underlyings and expirations may be desired.

Putting the two criteria together is also useful. Inflection points can be used in the process of determining a suitable parameter for the utility approach – by comparing observed marginal premiums around inflection points for options of underlying assets in a portfolio.